Image: www.math-only-math.com

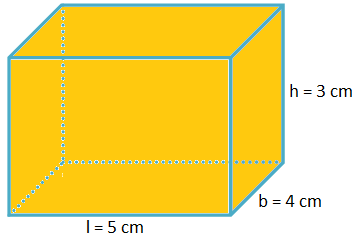
In geometry, a cuboid, also known as a rectangular prism, is a three-dimensional figure with six rectangular faces. Understanding the lateral surface area of a cuboid is crucial for calculating its total surface area and volume accurately. The lateral surface area refers to the combined area of the four rectangular sides of the cuboid. Grasping the concept of lateral surface area is fundamental in various fields, including engineering, architecture, and design. This detailed guide delves into the definition, formula, and practical applications of the lateral surface area of a cuboid.

Definition of Lateral Surface Area

The lateral surface area of a cuboid is the total area of its four rectangular sides, excluding the top and bottom faces. Unlike the total surface area, which includes all six faces, the lateral surface area considers only the sides of the cuboid.

Formula for Lateral Surface Area

The formula for calculating the lateral surface area (LSA) of a cuboid is given by:

LSA = 2(lh + wh)

Where:

• l represents the length of the cuboid
• h represents the height (or depth) of the cuboid
• w represents the width (or breadth) of the cuboid

Derivation of the Formula

To derive the formula, visualize the cuboid as a net, which is a two-dimensional representation of the three-dimensional shape. The net of a cuboid consists of four rectangular faces and two congruent rectangular bases. The lateral surface area includes the four rectangular faces, each with an area of lh or wh. Therefore, the total lateral surface area is twice the sum of these areas.

Practical Applications

Understanding the lateral surface area of a cuboid has several practical applications:

1. Architecture: Architects rely on the lateral surface area to calculate the paint or cladding required to cover the sides of buildings and structures.

2. Engineering: Engineers use the lateral surface area to determine the material needed to construct cuboids or rectangular containers for packaging, storage, and transportation.

3. Design: In product design, the lateral surface area helps designers determine the amount of material or fabric needed to create cuboid-shaped objects, such as furniture, appliances, and electronic devices.

Historical Context

The concept of the lateral surface area of a cuboid was developed in ancient geometry. Archimedes, a renowned Greek mathematician, played a significant role in the understanding and measurement of surface areas and volumes. His work laid the foundation for the formulas and calculations used in modern geometry.

Conclusion

The lateral surface area of a cuboid is a fundamental geometric concept with numerous practical applications. By thoroughly understanding the definition, formula, and historical context of the lateral surface area, we gain a valuable tool for calculations in various fields. Utilizing this knowledge empowers us to analyze and design three-dimensional structures and objects accurately and efficiently.

Image: learningcampusabend.z4.web.core.windows.net

What Is The Lateral Surface Area Of Cuboid