As we dive into the realm of geometry, let’s unveil the captivating world of circles and the areas they enclose. Exercise 12.2 of Class 10 Maths will guide us on an exciting journey through understanding the intriguing relationship between circles and areas.

Image: prigupta.blogspot.com
Circle, an enticing geometrical figure, has captured the fascination of mathematicians for centuries. Its unique properties and applications in problem-solving make it an essential concept in the study of geometry. Circles can be defined as round, two-dimensional shapes that have all points equidistant from a fixed center point, and the distance from the center to any point on the circle is called the radius.
Sector of a Circle
When we slice a pizza, we create a sector of a circle. A sector of a circle is a two-dimensional region bounded by two radii and the arc of a circle. The central angle subtended by the sector at the center of the circle determines its measurement, and the area is a fraction of the total area of the circle.
Let’s delve into the formulas for these areas. The area (A) of a sector of a circle is calculated as:
A = (θ/360°) πr2
where:
- θ is the central angle in degrees
- r is the radius of the circle in centimeters
Segment of a Circle
Imagine taking a slice of a pizza and removing the triangular portion—what remains is a segment of a circle. A segment of a circle is the area bounded by two radii and the intercepted arc. To find its area, we must take into account both the area of the sector and the area of the triangle formed by the radii and the chord.
The area (A) of a segment of a circle is given by:
A = (θ/360°) πr2 – (1/2)r2sinθ
where:
- θ is the central angle in degrees
- r is the radius of the circle in centimeters
Applications
Areas related to circles find practical applications in various fields, including:
- Architecture: Designing circular buildings, domes, and arches
- Engineering: Calculating the areas of gears, wheels, and bearings
- Art and Design: Creating circular patterns and motifs
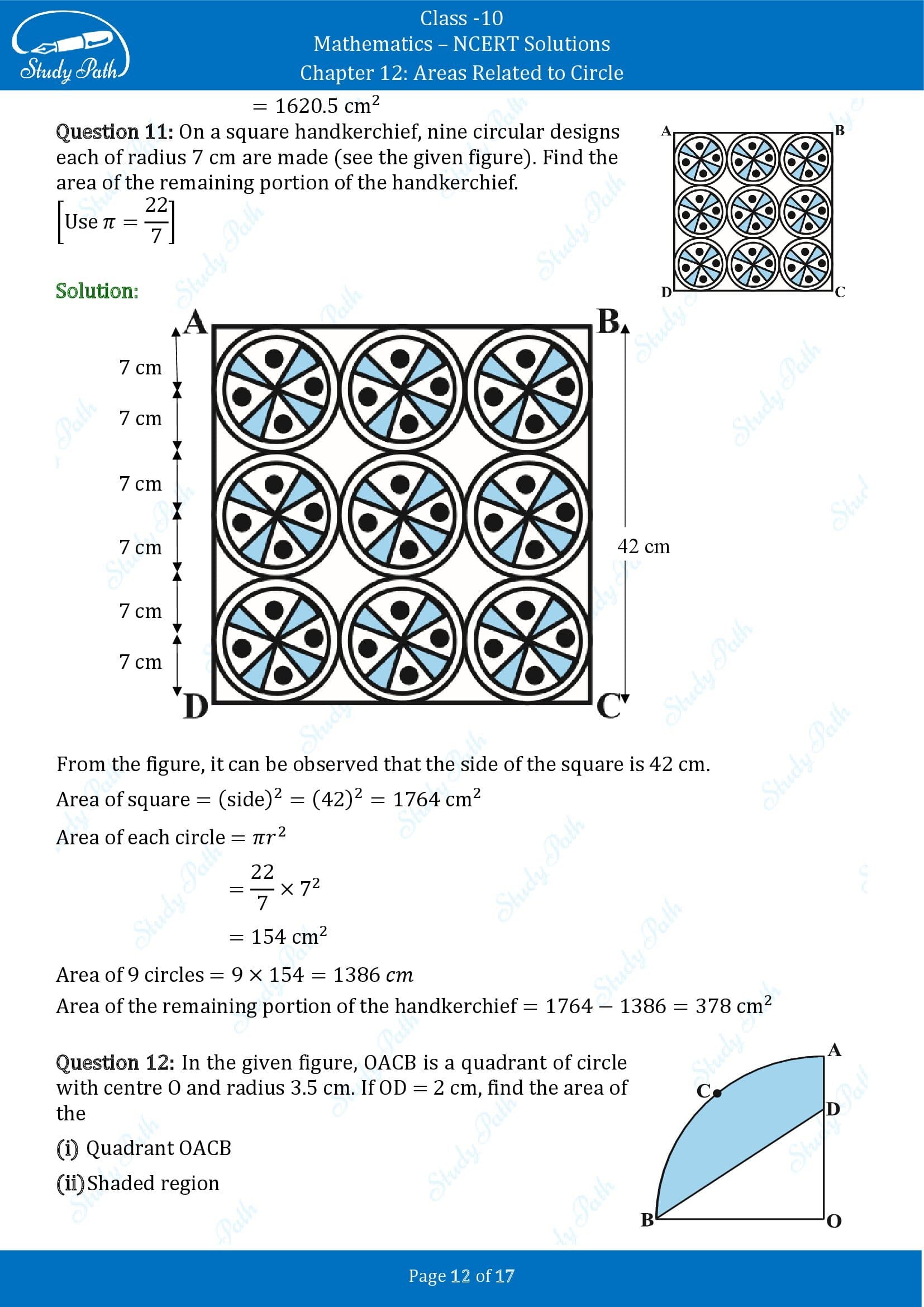
Image: www.thestudypath.com
Tips for Solving Problems
Here are some expert tips to help you conquer Exercise 12.2 problems:
- Understand the Concepts: Thoroughly grasp the definitions and formulas of sector and segment areas of circles.
- Convert Degrees to Radians: Remember to convert degrees into radians when applying the formulas, as π radians equals 180 degrees.
- Draw Diagrams: Sketching diagrams of the circles and sectors helps visualize the problem and identify relevant measurements.
Frequently Asked Questions (FAQs)
- What is the area of a complete circle?
- The area of a complete circle is πr2, where ‘r’ is the radius of the circle.
- How do I find the area of a quadrant of a circle?
- The area of a quadrant of a circle is one-fourth of the circle’s area. So, the area would be (πr2)/4.
- What is the difference between an area of a sector and an area of a segment?
- A sector of a circle is a region bounded by two radii and an arc, while a segment is the same region but with the area of the triangle formed by the radii and the chord subtracted.
Class 10 Maths Areas Related To Circles Exercise 12.2
Conclusion
Class 10 Maths Areas Related to Circles: Exercise 12.2 provides us with a solid foundation for understanding the concepts of sector and segment areas. This knowledge empowers us to solve problems in this domain effectively and aptly. Whether you are a learner eager to master the intricacies of circles or a teacher seeking to impart expert guidance, this guide serves as a comprehensive reference for exploring these geometrical wonders.

