1 and 3/4 as an Improper Fraction: A Comprehensive Guide to Understanding and Applying Fractions

An improper fraction is a fraction whose numerator is greater than or equal to its denominator. When it comes to 1 and 3/4, the conversion to an improper fraction is a straightforward journey. Simply multiply the whole number (1) by the denominator of the fraction (4) and add the numerator (3) to the result. So, 1 and 3/4 becomes (1 x 4) + 3 = 7/4. This improper fraction implies that we have 7 equal parts out of 4.

Historical Roots of Fractions

Fractions have a rich and fascinating history, with their origins dating back to ancient civilizations. The ancient Egyptians, known for their advanced mathematical prowess, developed a system of fractions based on unit fractions, where each fraction represented a specific part of a whole. The Babylonians, too, had their own system of fractions, using a base-60 system that allowed them to express fractions with great precision.

Applications of 1 and 3/4 in Real-World Scenarios

The improper fraction 7/4 finds practical applications in various spheres of life. In cooking, for instance, recipes often call for precise measurements of ingredients. A recipe that requires 1 and 3/4 cups of flour can be easily scaled up or down using the improper fraction 7/4. Similarly, in construction, architects and engineers use improper fractions to calculate ratios and proportions in building design.

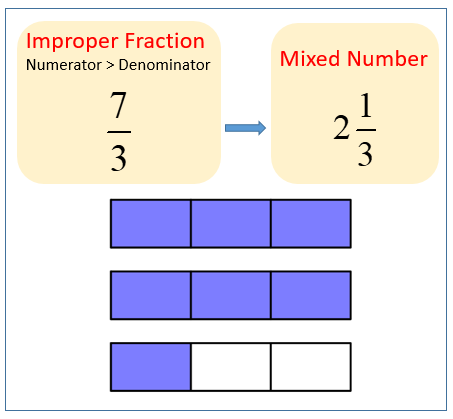
Image: www.onlinemathlearning.com

Insights from Experts: Understanding Fractions

Renowned mathematicians and educators have emphasized the importance of understanding fractions. Dr. Marilyn Burns, a leading expert in mathematics education, stresses that “fractions are the key to unlocking proportional reasoning and algebraic thinking.” By grasping the concept of fractions, we lay the groundwork for success in higher-level mathematics and quantitative disciplines.

Tips for Converting Mixed Numbers to Improper Fractions

Converting mixed numbers, like 1 and 3/4, to improper fractions is a valuable skill. Here’s a simple trick:

1. Multiply the whole number by the denominator of the fraction.
2. Add the numerator of the fraction to the result.
3. The sum you get is the numerator of the improper fraction, and the denominator remains the same as before.

For example, to convert 1 and 3/4 to an improper fraction, we do:

(1 x 4) + 3 = 7

So, 1 and 3/4 becomes 7/4.

1 And 3/4 As An Improper Fraction

Conclusion: The Power of Fractions

In conclusion, 1 and 3/4 as an improper fraction, 7/4, offers a versatile and practical way to represent parts of a whole. Understanding fractions empowers us to navigate the world of mathematics, from culinary creations to architectural marvels. Embrace the world of fractions and unlock the potential for deeper understanding and problem-solving in your daily life.