Differential equations are mathematical equations that relate a function to its derivatives. They play a fundamental role in various fields of science and engineering, such as physics, chemistry, and mechanics. However, finding the general solution of a differential equation can be a challenging task.
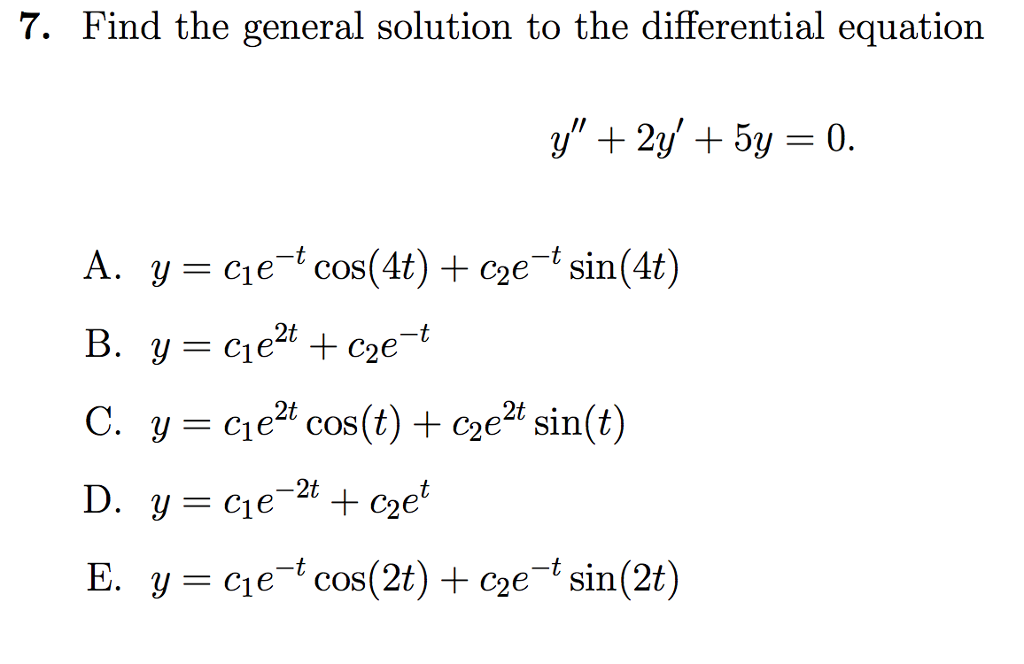
Image: www.chegg.com
The Anatomy of a Differential Equation
A differential equation is typically represented as:
dy/dx = f(x, y)
where y is the dependent variable, x is the independent variable, and f(x, y) is the function that relates them.
Order and Degree
The order of a differential equation refers to the highest derivative of the dependent variable that appears in it. The degree of a differential equation indicates the power of the highest derivative in the equation.
Linear and Nonlinear
Linear differential equations are those where the dependent variable and its derivatives are present only in the first power, and the coefficients are constants or functions of x only. Nonlinear differential equations, on the other hand, involve nonlinear functions of the dependent variable or its derivatives.

Image: www.numerade.com
Methods for Finding General Solutions
There are various methods available for finding the general solution of differential equations, including:
- Separation of Variables: This method applies to equations where the variables can be separated into separate functions of x and y.
- Integrating Factors: This method is used when the equation is not separable but can be made separable by multiplying both sides by an integrating factor.
- Exact Differential Equations: These equations are characterized by an equality of mixed partial derivatives and can be solved by finding a potential function.
- Homogeneous Differential Equations: Equations where both the function and its derivatives are homogeneous functions of x and y can be solved by substituting y = vx.
- Undetermined Coefficients: For linear nonhomogeneous equations with constant coefficients, this method involves finding a particular solution and the complementary solution to construct the general solution.
Expert Tips for Success
To enhance your ability in solving differential equations, consider the following expert advice:
- Master Basic Calculus: Differentiation and integration are fundamental skills essential for solving differential equations.
- Recognize Different Types of Equations: Understanding the type of differential equation you’re dealing with helps you choose the appropriate solution method.
- Practice Regularly: The key to proficiency is consistent practice. Solve as many equations as possible to improve your intuition.
- Seek External Resources: Utilize textbooks, online forums, and videos to supplement your understanding.
- Verify Your Solutions: After finding a potential solution, substitute it back into the original equation to verify if it holds.
FAQs
Q: What if I can’t find an exact solution?
A: Sometimes, it’s not possible to find an exact solution analytically. In these cases, numerical methods such as the Euler method or the Runge-Kutta method can be used to approximate the solution.
Q: How are differential equations used in real-life scenarios?
A: Differential equations have applications in a wide range of fields. For instance, they’re used to model population growth, describe the motion of objects, and analyze financial data.
How To Find General Solution Of Differential Equation
Conclusion
Finding the general solution of differential equations is a crucial skill that requires a combination of analytical thought and problem-solving abilities. By understanding the different methods and applying expert advice, you can develop your proficiency in solving these equations and delve deeper into the fascinating world of differential equations.
Have you found this information helpful in your pursuit of understanding general solution of differential equations? Let us know in the comments below!

