Do you ever wonder how architects design buildings that can withstand fierce winds or how engineers calculate the optimal shape for bridges to carry heavy loads? The answer lies in understanding the intricate world of geometry, particularly the ability to determine the area of triangles—a fundamental building block in countless applications. In this comprehensive guide, we will embark on a journey to unveil the secrets of finding the area of triangles, empowering you with the knowledge to tackle real-world challenges with confidence.
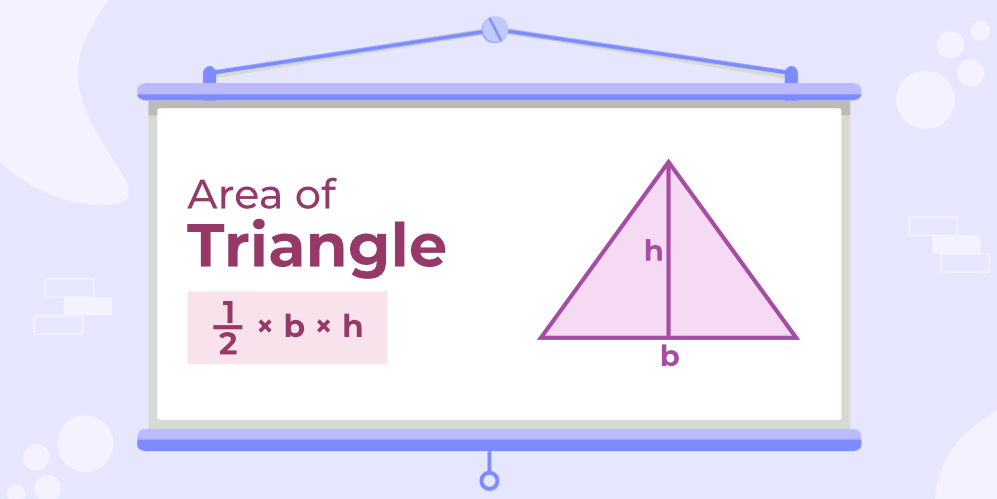
Image: www.geeksforgeeks.org
Unveiling the Essence of Triangles: A Geometrical Masterpiece
Triangles, characterized by their three sides and three angles, are ubiquitous throughout our world, from the towering pyramids of ancient Egypt to the intricate patterns in nature’s snowflakes. Their versatility extends beyond aesthetics, playing a pivotal role in fields as diverse as architecture, engineering, and art. However, it is the triangle’s area that truly unlocks its power. The area represents the amount of two-dimensional space enclosed within its boundaries, a crucial parameter in countless calculations.
Understanding how to find the area of a triangle is not merely an academic pursuit but an invaluable skill that unlocks a world of possibilities. Whether you’re a student navigating the complexities of geometry, an architect designing awe-inspiring structures, or an artist seeking to create harmonious compositions, mastering this concept will elevate your endeavors and empower you to achieve remarkable outcomes. Embrace this journey of discovery, and together, we will conquer the art of finding the area of any triangle with precision and finesse.
Delving into the Treasure Trove of Triangle Area Formulas
As we delve into the enchanting realm of triangle geometry, we will encounter two distinct yet equally valuable formulas that serve as our guiding lights in calculating the area. These time-tested formulas have stood the test of time, empowering mathematicians, engineers, and artists alike to solve countless problems with remarkable accuracy.
- The Base and Height Formula: A Timeless Classic
This formula, often referred to as the “base and height” formula, is renowned for its simplicity and straightforward application. To calculate the area ( denoted as “A” ) of a triangle using this method, we simply multiply the length of its base ( denoted as “b” ) by its corresponding height ( denoted as “h” ) and divide the result by two. Expressed mathematically, it translates to:
A=(1/2)xh xb
- The Heron’s Formula: A Masterpiece of Versatility
While the base and height formula shines in its simplicity, Heron’s formula emerges as the champion when dealing with triangles where identifying the base and height poses a challenge. This formula, attributed to the brilliant mathematician Heron of Alexandria, allows us to determine the area of a triangle using only the lengths of its three sides, denoted as “a,” “b,” and “c.” Heron’s formula unveils its brilliance through the following equation:
A=√s(s-a)(s-b)(s-c)
where “s” represents the semi-perimeter of the triangle, calculated as the sum of its three sides divided by two.
Unveiling the Secrets of Side Length Measurement: A Critical Skill
Before we can embark on the quest to find the area of a triangle, it is imperative to master the art of accurately measuring its sides. Precision in this aspect is paramount to ensure reliable area calculations.
- Ruler Mastery: A Foundation of Accuracy
For triangles with readily accessible sides, a ruler serves as an indispensable tool. Carefully align the ruler’s edge with the base of the triangle and note the measurement in the desired unit, be it inches, centimeters, or any other relevant unit. Repeat the process for the height, measuring perpendicularly from the base to the opposite vertex.
- Protractor Precision: Unraveling Angles with Confidence
When faced with triangles where direct side measurement is impractical or impossible, a protractor steps into the spotlight as our trusted ally. This remarkable tool allows us to measure angles with high accuracy. Position the protractor such that its center aligns with the vertex of the triangle, and its baseline coincides with one side. Note the angle measurement in degrees, paying close attention to the markings and ensuring a precise reading.
- Trigonometry’s Power: Unveiling Hidden Side Lengths
The world of trigonometry unfolds a treasure trove of techniques that empower us to determine side lengths even when direct measurement is not feasible. By employing trigonometric ratios like sine, cosine, and tangent, we can harness the power of angles to deduce the unknown sides of a triangle with remarkable precision.
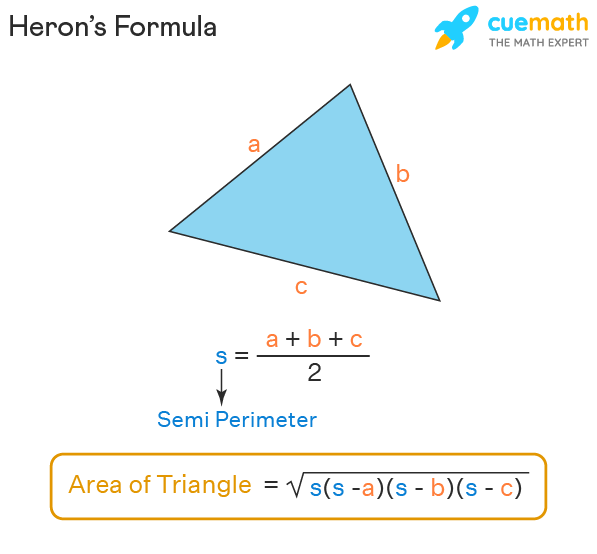
Image: notariaurbina.cl
Find The Area Of The Following Triangle
Exceptional Examples: Illuminating the Path to Mastery
To fully grasp the intricacies of finding the area of triangles, let’s illuminate our understanding with a series of thought-provoking examples.
- The Equilateral Triangle: A Paragon of Symmetry
An equilateral triangle, captivating in its harmony, boasts equal side lengths and angles. This remarkable symmetry simplifies the area calculation, allowing us to leverage the base and height formula effortlessly. By simply squaring the length of one side and multiplying by the square root of 3 over 4, we unveil the area of this equilateral beauty.
- The Right Triangle: A Gemstone of Geometry
A right triangle, adorned with its 90-degree angle, presents a unique opportunity to utilize the Pythagorean theorem as our trusty guide. Once we determine the lengths of the two shorter sides, known

