In the realm of calculus, derivatives hold immense significance as they provide the means to analyze the rate of change of functions. Understanding how to derive functions is crucial for unlocking the mysteries of calculus and its applications in various scientific disciplines. In this article, we will embark on a journey to uncover the derivative of the trigonometric function tan x using the fundamental approach known as the first principle.

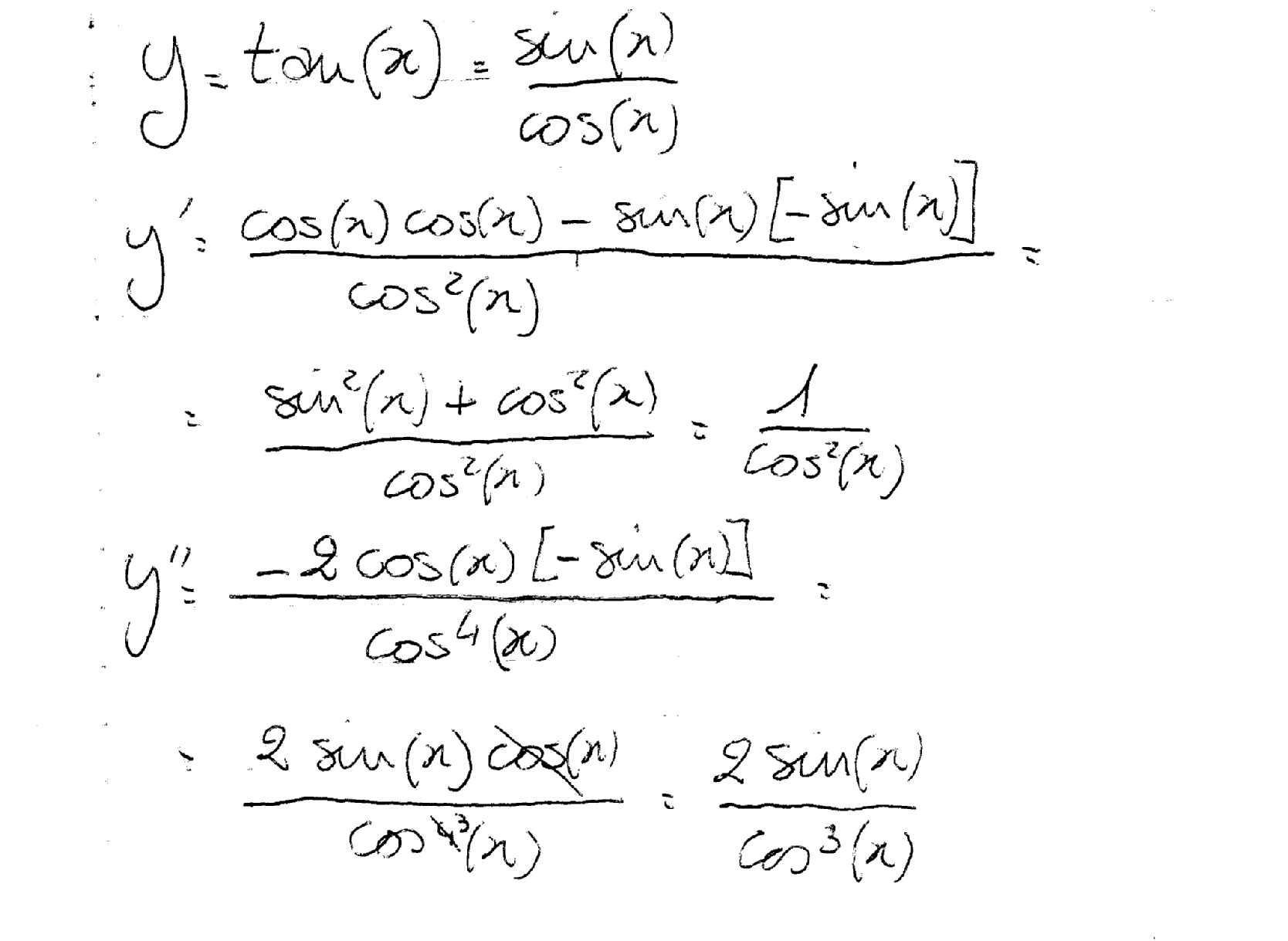
Image: iteducationlearning.com

Grasping the Notion of Derivatives

Before delving into the derivation process, let’s establish a clear understanding of the concept of derivatives. Simply put, the derivative of a function describes its instantaneous rate of change at any given point. Visualize a car traversing along a winding road—the derivative at a particular instant tells us the car’s speed and the direction in which its speed is changing.

The Essence of First Principle

The first principle approach to finding derivatives involves the computation of the limit of the difference quotient. For a function $f(x)$, the difference quotient is given by

$$\fracf(x+h)-f(x)h$$

where $h$ is a small increment. The derivative is then obtained as we take the limit of this difference quotient as $h$ approaches zero:

$$f'(x)=\lim_h\to 0\fracf(x+h)-f(x)h$$

Image: www.youtube.com

Find The Derivative Of Tan X From First Principle

Calculating the Derivative

Equipped with this understanding, let’s embark on the process of finding the derivative of tan x. The function tan x is defined as the ratio of sine to cosine: \ [tan x = \fracsin xcos x\]

Using the definitions of sine and cosine from the unit circle, we get:

$$tan x = \fracyx$$

where $(x,\; y)$ are the coordinates of a point on the unit circle.

Now we can calculate the difference quotient for tan x:

$$\fractan (x+h) – tan xh$$

$$=\frac\fracsin (x+h)cos (x+h) – \fracsin xcos xh$$

$$=\fracsin (x+h)cos x – sin x cos (x+h)hcos x cos (x+h)$$

This expression may appear formidable, but with careful manipulation, we can simplify it:

$$=\fracsin x cos h + cos x sin h – sin x cos hhcos x cos (x+h)$$

$$=\fraccos x sin hhcos x cos (x+h)$$

$$=\fracsin hhcos (x+h)$$

Finally, we take the limit as $h$ approaches zero, yielding the derivative of tan