In the realm of mathematics, exponents hold a power of their own, capable of transforming complex calculations into simple strokes of brilliance. Join us as we embark on a journey to demystify the laws of exponents, equipping you with the tools to conquer these mathematical challenges with confidence and ease.

Image: lessonliblehner.z21.web.core.windows.net
Exponents, often represented as small numbers perched superscript above a base, serve as a shorthand notation for repeated multiplication. They empower us to express daunting products in a compact and manageable form. Let’s dive into a specific example to illuminate the essence of exponents. Take the expression 23, where 2 represents the base and 3 is the exponent. Here, the exponent indicates that we multiply the base (2) by itself three times:
23 = 2 2 2 = 8
This elegant notation allows us to swiftly determine the result without resorting to arduous long multiplication.
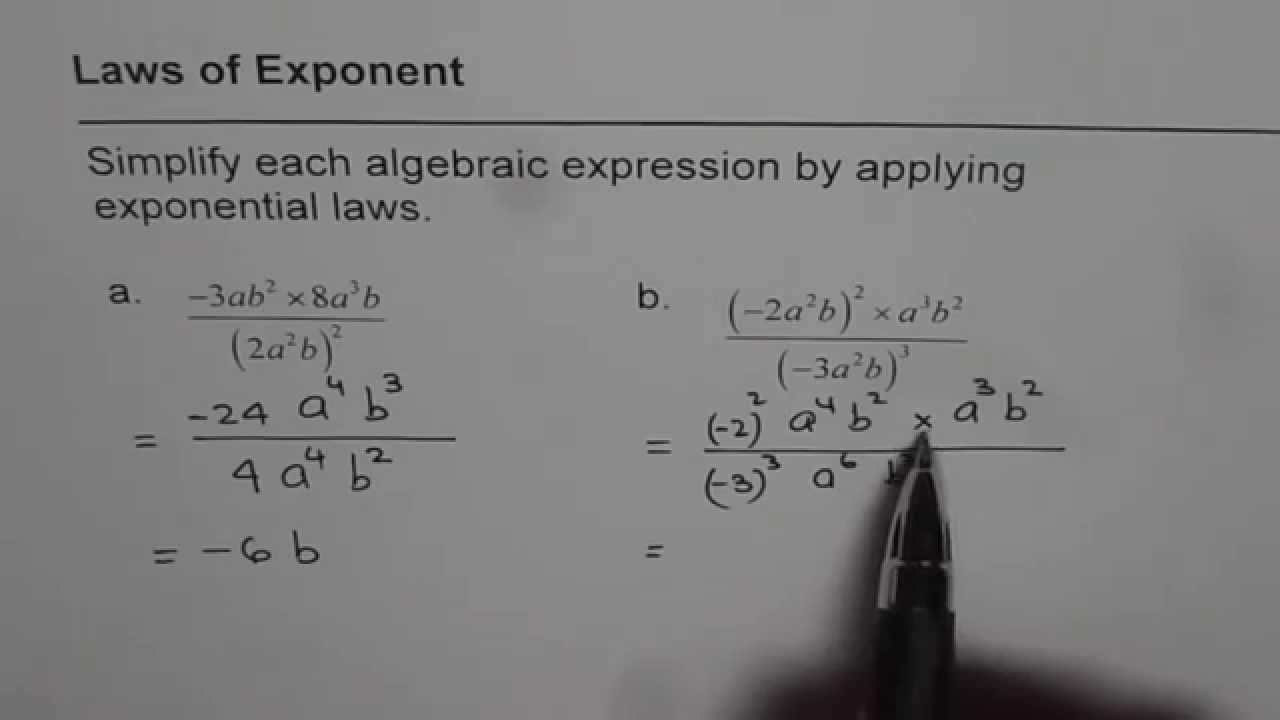
Image: www.youtube.com
Simplify The Following Using Laws Of Exponents
The Laws of Exponents: A Pathway to Simplicity
Navigating the world of exponents becomes effortless when armed with a set of fundamental laws that streamline our operations. These laws hold the key to simplifying complex expressions, transforming intricate equations into approachable computations.
Law 1: Multiplication of Exponents with Same Base
When multiplying exponents with identical bases, we simply add their respective exponents. For instance:
am an = a(m+n)
In simpler terms, multiply the bases and add the exponents.
Law 2: Division of Exponents with Same Base
The division of exponents with equivalent bases follows a similar rule. Subtract the exponent of the denominator from the exponent of the numerator, yielding the new exponent of the quotient. This mathematical dance goes like this:
am / an = a(m-n)
Law 3: Powering an Exponent
When an exponent is raised to another exponent, we multiply the exponents together to arrive at the final exponent. This operation takes the form:
(am)n = a(mn)
In essence, multiply the exponents and leave the base unchanged.
Law 4: Zero Exponent
In the world of exponents, zero holds a special status. Any base elevated to the power of zero always equals one, regardless of the numerical value of the base:
a0 = 1
Law 5: Negative Exponents
Negative exponents invite us to flip the fraction. We reciprocate the base and convert the

