“The enigmatic world of numbers holds countless secrets, each beckoning us to unravel its hidden truths.”

Image: www.cuemath.com

Embracing the Prime Factorization Method

Today, we embark on a mathematical odyssey to uncover the elusive cube root of 2744, a task we shall accomplish through the esteemed technique of prime factorization. Immerse yourself in this intriguing journey as we dissect the intricacies of this enigmatic number and witness its underlying mathematical harmony.

Defining the Elusive Cube Root

Before delving into our mathematical exploration, let us illuminate the concept of the cube root. A cube root, by definition, is a number that when multiplied by itself three times, yields the original number. Consider the analogy of crafting a cube-shaped box. To determine the length of each side of the cube, you must find the cube root of the volume of the box. This concept holds true for our quest today: finding the cube root of 2744 is akin to determining the side length of a cube with a volume equivalent to 2744 cubic units.

Deciphering the Prime Factorization Method

The prime factorization method, an invaluable mathematical tool, grants us the ability to break down complex numbers into their fundamental building blocks – prime numbers. Prime numbers, as the very essence of numbers, are those divisible only by themselves and the number one. This method proves especially potent for our mission of finding the cube root of 2744.

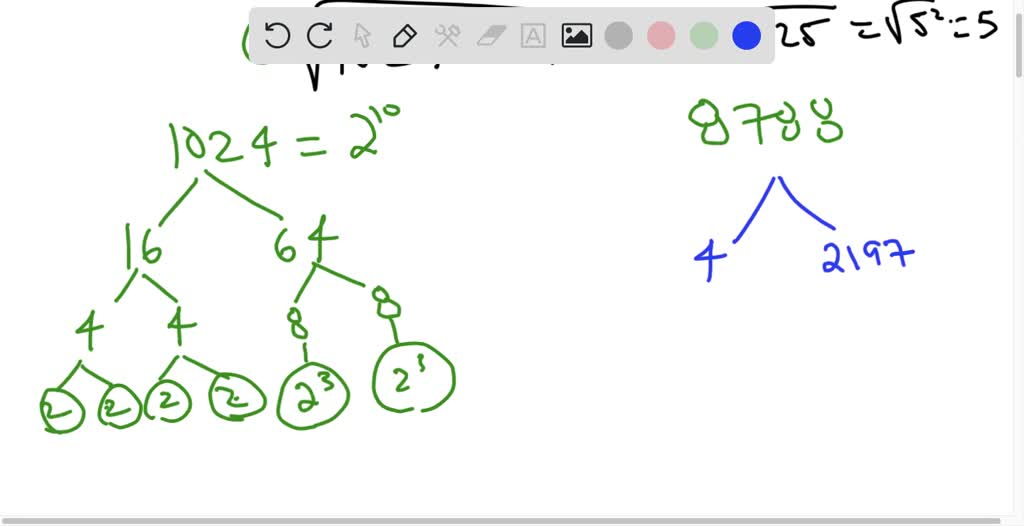
Image: www.numerade.com

Step-by-Step Prime Factorization

Let us now don the mantle of mathematical explorers and embark on the prime factorization of 2744. Commence this journey by repeatedly dividing 2744 by the smallest prime numbers until you arrive at a prime factor that no longer divides evenly. Document each division and the corresponding prime factor:

• 2744 ÷ 2 = 1372
  2 is a prime factor
• 1372 ÷ 2 = 686
  2 is a prime factor
• 686 ÷ 2 = 343
  2 is a prime factor
• 343 ÷ 7 = 49
  7 is a prime factor
• 49 ÷ 7 = 7
  7 is a prime factor
• 7 is prime and cannot be further divided

Behold, the prime factorization of 2744 unveils its secrets:

$$2744 = 2 \times 2 \times 2 \times 7 \times 7 \times 7$$

Extracting the Cube Root via Prime Factorization

Armed with the prime factorization of 2744, we now possess the key to unlocking its cube root. Here’s the formula that illuminates the path:

$$\sqrt[3]2744 = \sqrt[3]2^3 \times 7^3$$

Using this formula as our guide, we can determine the cube root:

$$\sqrt[3]2744 = 2 \times 7 = 14$$

Therefore, the cube root of 2744, the enigmatic number we sought to uncover, is revealed to be the more approachable 14. It is through the ingenious prime factorization method that we have successfully unraveled this mathematical mystery.

Tips and Expert Advice for Mathematical Explorers

Unveiling the cube root may be akin to embarking on a captivating adventure, but we must approach it with strategy and precision. The tips and advice we present shall empower you to navigate the enigmatic world of numbers with ease and confidence.

• Embrace the prime factorization method: As exemplified in today’s mathematical endeavor, prime factorization serves as a versatile tool for comprehending and dissecting complex numbers. Its ability to unravel numbers into their prime components grants us the power to decipher their most intricate secrets.
• Seek mentors and embrace collaboration: Engage with fellow mathematical enthusiasts, seek guidance from experienced mentors, and participate in online forums. Exchanging ideas and perspectives not only enriches your understanding but also sparks innovative approaches to problem-solving.
• Practice relentlessly: Consistency is the key to mathematical mastery. Dedicate time to practicing various cube root strategies and tackling a diverse range of numerical challenges. This dedication will sharpen your skills and expand your mathematical toolkit.

FAQs on the Cube Root

To further illuminate your understanding of the cube root and the techniques surrounding it, we present a curated selection of frequently asked questions:

Q: What is the cube root of a number?

Answer: The cube root of a number is the value that, when multiplied by itself three times, results in the original number. For instance, the cube root of 27 is 3, since 3 x 3 x 3 = 27.

Q: How is the prime factorization method used to find the cube root?

Answer: Prime factorization involves breaking down a number into its prime factors. The cube root of the number can then be determined by grouping the prime factors into sets of three and taking the product of the cube roots of each group.

Q: What are some tips for finding the cube root quickly and accurately?

Answer: Estimating the cube root is a useful starting point. For instance, if you are finding the cube root of 2744, you can estimate it to be around 14 (since 14 x 14 x 14 ≈ 2744). You can then use methods like successive approximation or the Babylonian method to refine your estimate and find the exact cube root.

Find The Cube Root Of 2744 By Prime Factorization Method

Conclusion

Our exploration of the cube root of 2744 has illuminated the profound depths of mathematical beauty and ingenuity. Through the lens of prime factorization, we have unveiled the secrets of this enigmatic number, transforming it from an abstract entity into a comprehensible concept.

As you continue your mathematical journey, remember that curiosity and perseverance are your unwavering companions. Embrace the challenges that lie ahead, for they are the stepping stones to mathematical mastery. Should the topic of the cube root pique your interest, delve deeper into its intricacies, unraveling its mysteries through exploration and discovery.

Join the captivating world of numbers and unravel their hidden truths. Are you ready for your next mathematical adventure?

“`