In the realm of mathematics, numbers hold countless secrets and surprises. Among them, the least common factor holds a special allure, connecting seemingly disparate values through a shared mathematical thread. Embark on a numerical expedition as we uncover the intricacies of the least common factor, particularly focusing on the intriguing case of 9 and 15.

Image: www.pinterest.com
The least common factor, or LCM for brevity, is an integral concept in number theory, playing a pivotal role in various mathematical endeavors. It represents the elusive “sweet spot” where several numbers gracefully intertwine, sharing the smallest value that can be divided evenly by each of them.
To delve into the depths of this concept, let us turn our attention to the specific case of 9 and 15. Seeking their least common factor, we embark on a meticulous analysis of their inherent traits. The number 9, often hailed as an enigmatic single-digit integer, boasts a composition of three prime factors: 3 x 3. On the other hand, its enigmatic counterpart, 15, emerges as the esteemed product of three distinct prime factors: 3 x 5.
With this knowledge at our disposal, the path to unraveling their least common factor becomes increasingly discernible. Ingeniously combining the shared prime factor, 3, and the distinctive prime factor, 5, we arrive at the elusive LCM, which stands at a humble 15. This outcome elegantly underscores the fundamental role of prime factorization in determining the least common factor.
Venturing beyond the realm of theory, the least common factor finds widespread application in a myriad of real-world scenarios, leaving an indelible mark on our daily lives. Consider the task of juggling multiple musical rhythms, each with its unique cadence. The least common multiple, a concept closely intertwined with the least common factor, acts as a guiding light, revealing the tempo at which all rhythms synchronize harmoniously.
Similarly, in the bustling world of construction, the least common factor holds sway. Envision a scenario where both wooden planks and metal beams, measuring 9 feet and 15 feet respectively, must be cut into equal-sized segments. By determining the least common multiple, we glean the optimal cutting length, ensuring efficient and precise construction. These diverse applications underscore the practical significance of the least common factor, highlighting its far-reaching impact.
As we conclude our mathematical odyssey, let us pause and reflect upon the intriguing journey undertaken to unravel the least common factor of 9 and 15. From the theoretical underpinnings to the practical implications, this exploration has shed light on a concept that plays a vital role in our everyday lives, connecting the world of numbers to tangible experiences. May this newfound knowledge empower you to conquer future mathematical challenges with newfound confidence and enthusiasm.
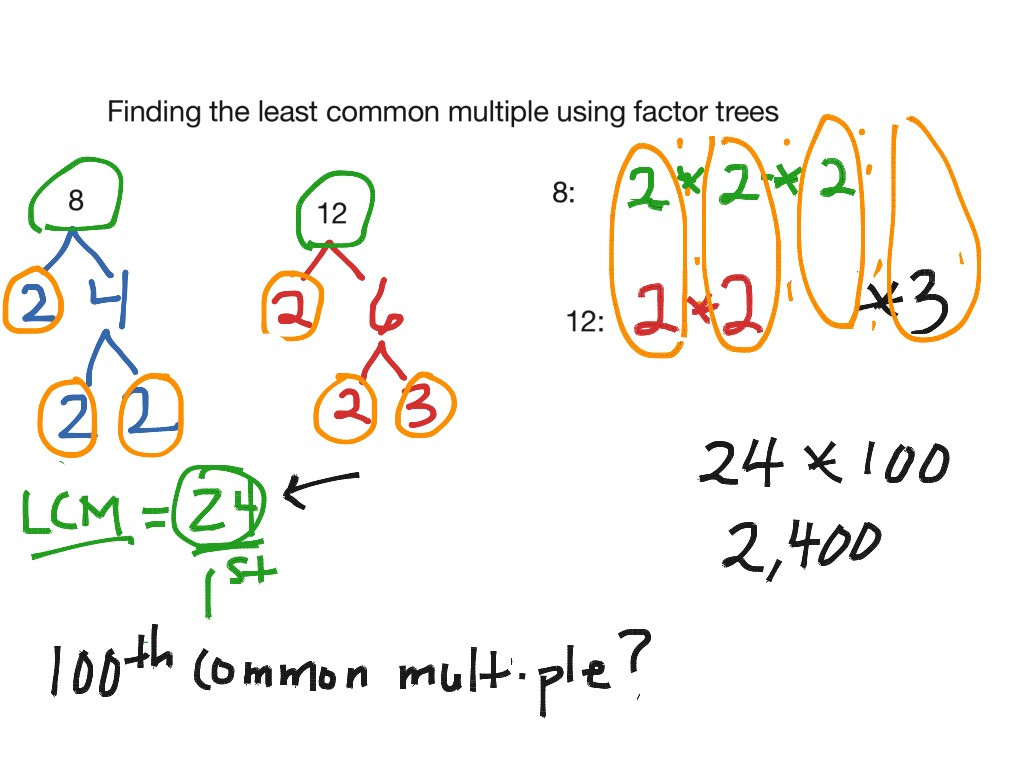
Image: www.showme.com
Least Common Factor Of 9 And 15

