As a math enthusiast, I always loved unraveling the mysteries of numbers. One concept that fascinated me was the relationship between mean, median, mode, and class. Through this blog post, I aim to shed light on this intriguing subject, making it accessible to all inquisitive minds.

Image: www.vrogue.co
Exploring the Statistical Measures
Mean
Mean, also known as average, represents the sum of all values in a dataset divided by the number of values. It provides an indication of the central tendency of the data.
Median
Median is the middle value of a dataset when arranged in ascending or descending order. Unlike mean, median is not affected by outliers or extreme values.
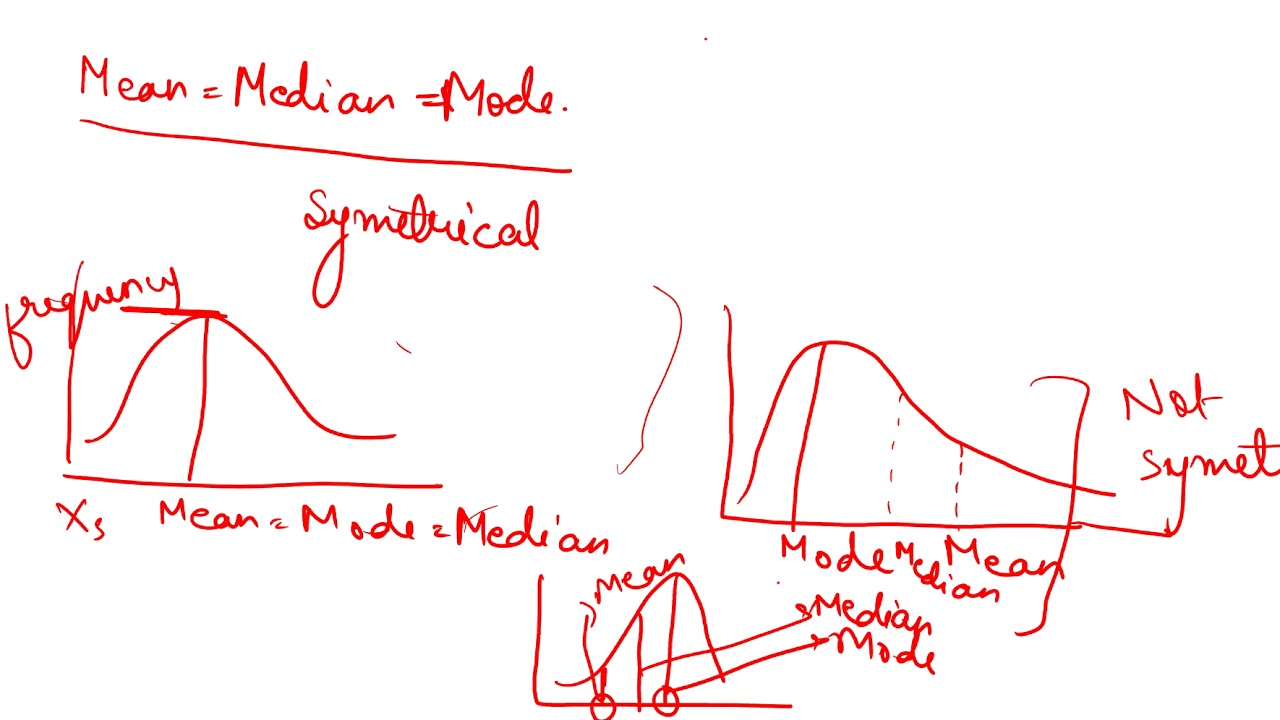
Image: www.vrogue.co
Mode
Mode is the value that appears most frequently in a dataset. It indicates the most common value, and a dataset can have multiple modes.
Class
Class in statistics refers to a grouping of data points into intervals or categories. It helps organize and summarize large datasets and makes data interpretation easier.
Understanding the Distinctions and Interdependencies
While mean, median, mode, and class are all measures of central tendency, they have distinct characteristics. Mean considers all data points, whereas median and mode consider only the middle value or most frequent value, respectively. Class, on the other hand, does not measure central tendency but facilitates data categorization and analysis.
The choice of which measure to use depends on the nature of the dataset and the specific questions being asked. In some cases, mean provides the most representative value, while in others, median or mode might be more appropriate. Understanding these measures and their interdependencies enhance our ability to make informed conclusions from data.
Applications in the Real World
The relationship between mean, median, mode, and class has practical applications in various fields:
- In economics, mean household income and median income provide distinct perspectives on income distribution.
- In education, the class of students within a grade level represents a distinct group based on age or academic achievement.
Grasping these concepts enhances our analytical skills and enables us to make informed decisions based on data interpretation.
Tips for Effective Data Analysis
- Identify the research question to determine the most appropriate measure of central tendency.
- Consider the distribution of data and the presence of outliers when choosing between mean, median, or mode.
- Use class intervals to group data sensibly and draw meaningful conclusions.
Frequently Asked Questions (FAQs)
Q: What is the difference between mean and median?
A: Mean considers all values, while median considers only the middle value, making it less sensitive to outliers.
Q: When should I use mode instead of mean or median?
A: Use mode to identify the most common value when data is categorical or has multiple peaks.
Q: How does class size affect data analysis?
A: Choosing appropriate class size ensures that data is grouped effectively for meaningful analysis and avoids losing valuable information.
Relation Between Mean Median And Mode Class 10
Conclusion
Understanding the interrelationship between mean, median, mode, and class empowers us to comprehend and analyze data effectively. By recognizing their distinctions and applications, we can make informed choices when interpreting and communicating data. I encourage you to explore these concepts further and delve into their fascinating world. Share your thoughts and questions about this topic in the comments below.

