Introduction:

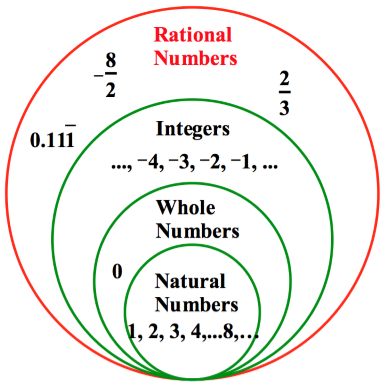
Image: www.myxxgirl.com

Have you ever pondered the vastness of numbers between two seemingly separate numbers? The world of numbers extends far beyond the familiar integers; within the realm of rational numbers, a universe of infinite possibilities unfolds. This article embarks on a journey to delve into the fascinating concept of rational numbers, exploring the countless numbers that reside between any two rational numbers. Join us as we unravel the secrets of this intricate mathematical tapestry.

Defining Rational Numbers: A Prelude to Infinity

Rational numbers lie at the heart of mathematics, representing a set of numbers that can be expressed as the quotient of two integers. Unlike irrational numbers, such as the enigmatic pi, rational numbers can be precisely represented as simple fractions. They form a dense network, filling the number line with an abundance of possibilities. Every rational number can be visualized as a point on this infinite line.

Between Any Two Rational Numbers: Dwelling in the Interplay of Density

The remarkable property of rational numbers lies in their dense nature. Between any two distinct rational numbers, no matter how close together, an infinite number of other rational numbers reside. This mesmerizing phenomenon stems from the fact that between any two numbers, we can always find their arithmetic mean, effectively creating a new rational number. This recursive process of finding means can be repeated indefinitely, generating an endless stream of rational numbers within the given interval.

A Journey Through Examples: Illuminating the Plenum of R

For a vivid illustration, let us consider the two rational numbers 1/3 and 1/2. Between these numbers, we can locate 1/4 (the arithmetic mean of 1/3 and 1/2). Continuing this process, we discover 3/8 (the mean of 1/4 and 1/2), followed by 5/16, and so on. This infinite sequence of rational numbers, nestled between 1/3 and 1/2, exemplifies the inexhaustible nature of rational numbers within any interval.

Cantor’s Theorem: Unveiling a Puzzling Paradox

The philosopher and mathematician Georg Cantor’s profound theorem sheds light on the uncountable nature of rational numbers. Cantor demonstrated that while the set of natural numbers is countably infinite, the set of rational numbers is uncountably infinite. This perplexing paradox arises from the fact that the rational numbers, despite their dense distribution, can be paired one-to-one with the uncountable set of real numbers. This fascinating relationship underscores the vastness of the rational number system.

Rational Numbers in the Limelight: Applications in Real-World Scenarios

Rational numbers play an indispensable role in a diverse array of real-world applications, spanning scientific research to everyday problem-solving. From calculating batting averages in sports statistics to devising accurate ratios for chemical mixtures, rational numbers form the foundation of our understanding. Their ability to represent precise fractional values makes them essential tools in fields such as engineering, medicine, economics, and beyond.

Conclusion: Embracing the Abundance of Rational Numbers

Our exploration has unveiled the unparalleled richness of rational numbers, revealing an infinite realm of numerical possibilities between any two given rational numbers. This profound attribute serves as a reminder of the boundless wonders that mathematics holds. As we continue to unravel the intricate tapestry of numbers, the enigmatic nature of rational numbers will undoubtedly continue to inspire and intrigue mathematicians and scholars for generations to come.

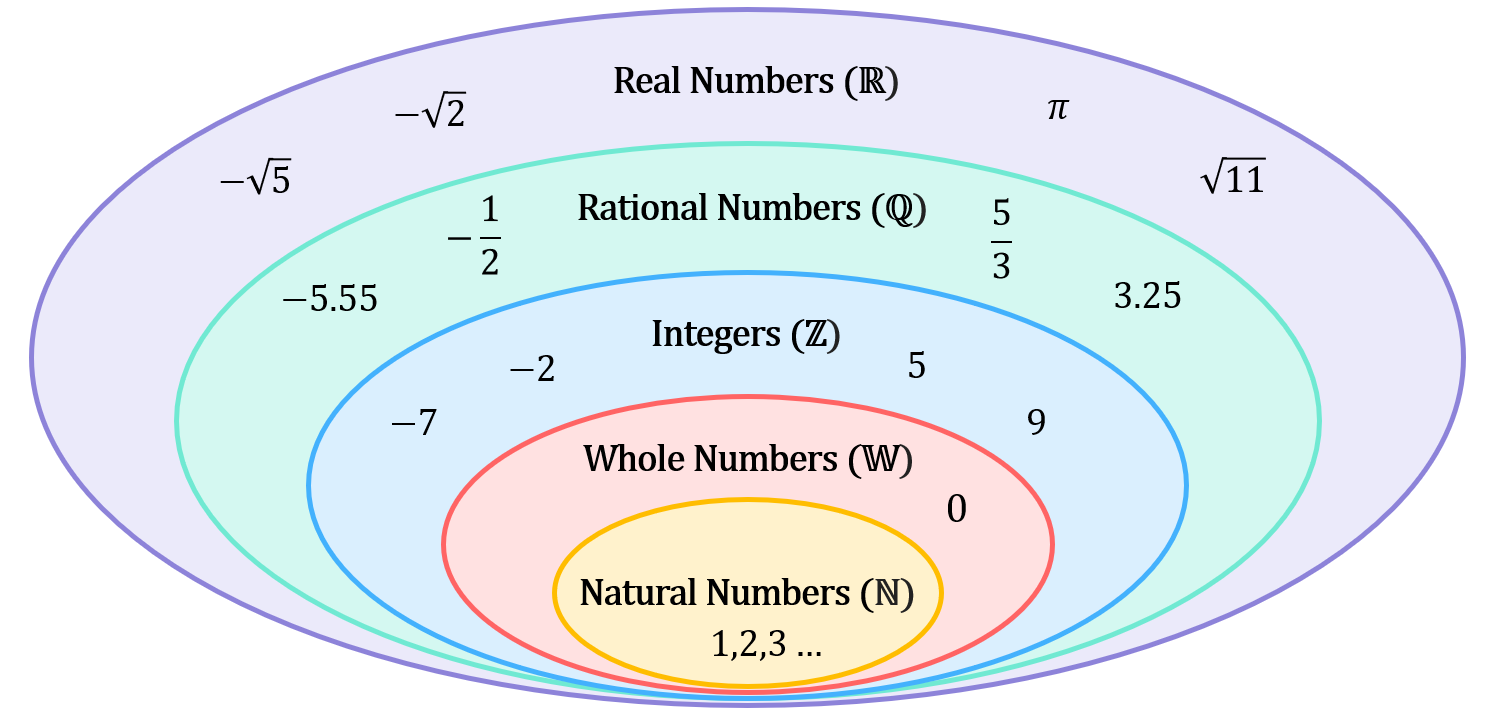
Image: www.national5.com

How Many Rational Numbers Are There Between Two Rational Numbers